PoTM - Emergent World Representations - Exploring a Sequence Model Trained on a Synthetic Task

I recently came across an interesting paper that got accepted at ICLR 2023: Emergent World Representations: Exploring a Sequence Model Trained on a Synthetic Task (Li et al.). It provides valuable insights toward the understanding of black-box language model. Specifically, by training a LM to play a chess-like game, Othello, without feeding it any knowledge of the game rules, they discover that LM does learn meaningful latent representations that help it uncover the game and make legal disc moves on the board.

Table of Contents

• The Othello game
• Teach LM to play Othello
  • Observation 1: LM respects the game’s rule.
  • Observation 2: Hidden representations encoded in LM’s layers represent the board’s states
  • Observation 3: The relationship between model’s internal representation (or board state, thanks to observation 2) and model’s prediction (i.e next legal move) is causal.

The Othello game

(Source: https://github.com/SiyanH/othello-game)

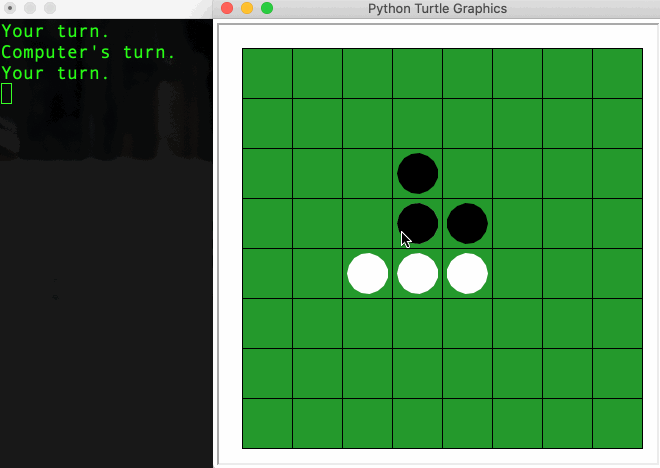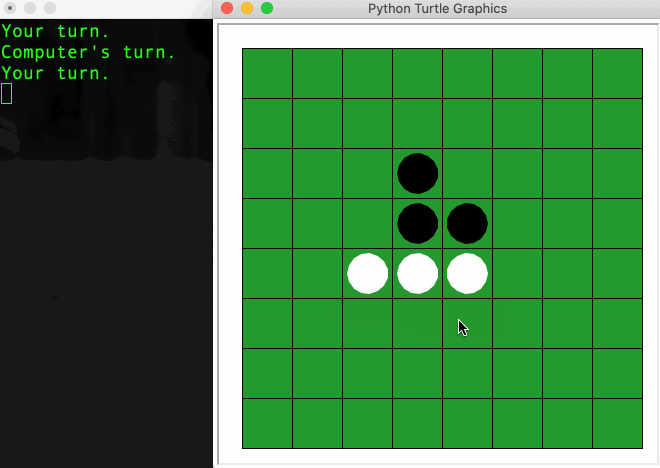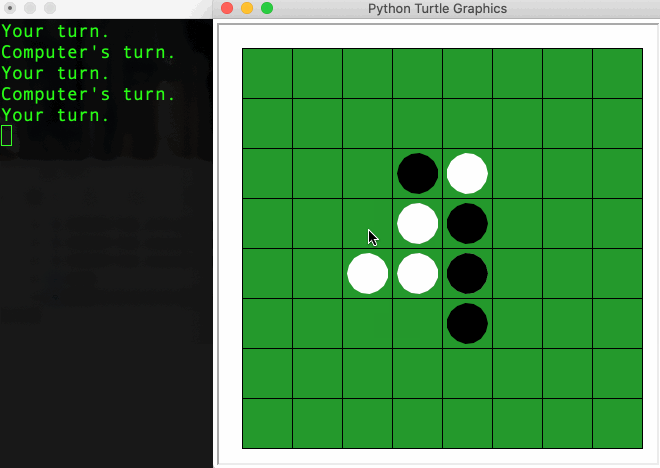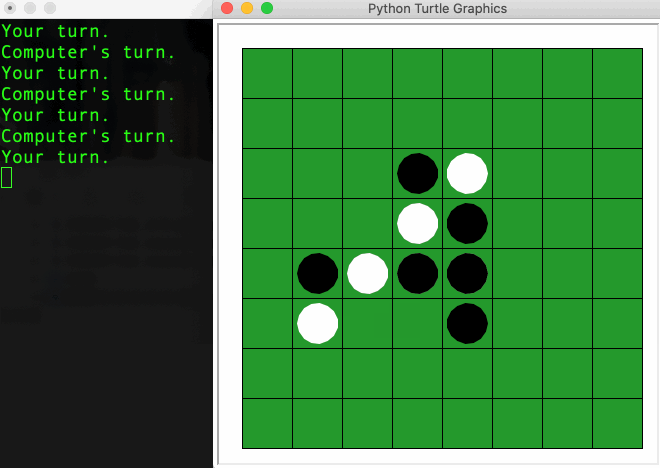
Two players, one holding black discs, one holding white discs, take turns making a move (aka. placing their colored disc) on the 8x8 board. The goal is to cover the board with the majority of their color. When a player makes a move, any opponent’s disc found in between (horizontally, vertically or diagonally) the disc his just placed and any of existing discs of his color will be flipped over to become their own color. A legal move is a move that ensures at least one such flip happens. Otherwise, the game ends.

A casual LM is trained to play Othello and its internal representation will be analyzed. Author chooses this game as it is simple enough while still has a sufficiently large solution space (aka. where to move given the board’s current state) to avoid memorization.

Teach LM to play Othello

The LM is fed a naive transcript recording interleaving moves of two players without adding the game rules or additional analysis of game state (e.g. [F5, C5, …] where F, C are vertical indices, and 5 is horizontal index of the board)). It has to figure out who play next and identify which tiles on the board are legal to move to.

Observation 1: LM respects the game’s rule.

The trained LM respects the game rule, it can predict the next legal move with very low error rate according to the current state of the board. (Note: a legal move is not necessary an optimized move as the model is not trained to win the game). This is not due to the memorization as the test set is ensured not to be seen during the training.

Observation 2: Hidden representations encoded in LM’s layers represent the board’s states

Board state involves whether each tile holds a black disc or a while disc or is empty. Author trains a non-linear MLP classifier \(p_{\theta}(x)\), taking in the internal activations \(x\) of a specific layer of LM, at a given game step, as features and yielding one of three labels: {black, white, empty}. In this way, they seek to investigate whether there is a mapping between LM’s internal representations and board’s states. Indeed, the results show that the classifier achieves high accuracy, implying such mapping exists.

Observation 3: The relationship between model’s internal representation (or board state, thanks to observation 2) and model’s prediction (i.e next legal move) is causal.

In other words, changes in the network’s activations, leading to changes in board’s states according to observation 2 (e.g. a tile is switched from black to white), will causally cause the model to predict a move from a new set of possible legal moves in compliance with new board state.

For example, in the figure below, from lower left board to lower right board, network’s activations has been intervened to switch the tile E6 from black to white. Consequently, the set of next possible legal moves has to be changed from {B4, C6, D3, E7, F4, F6} (upper left) to {B3,B4,C6,D3,F4} (upper right). The model predicts correctly this new set.

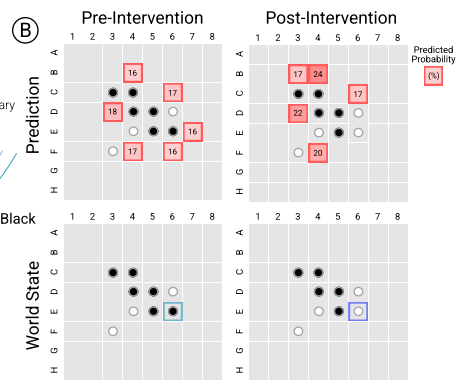(Source: copied from the paper)

Question arises: how to modify the network’s activations \(x\) such that the tile E6 switches from black to white while others keep intact ? (we denote current board state as \(B\), new board state as \(B'\) and \(B'\) differs from \(B\) only at tile E6)

• Pre-define a layer index \(l_s\), all activations from the layer \(l_s\) until the final layer, at the last game step, will be modified, as in figure below:

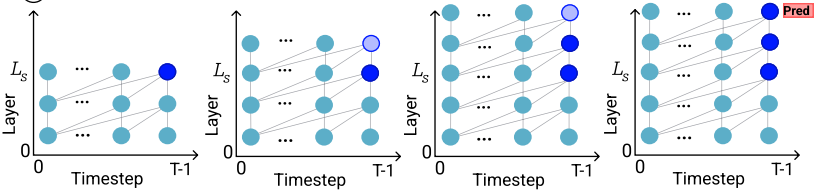  (Source: copied from the paper)

  Author argues that the intervention at only one layer \(l_s\) is not effective, as the change made at layer \(l_s\) will be diluted when it reaches the last layer, making the output being not affected by the change.

• The network’s activations \(x\) is updated in gradient descent manner such that new \(x'\) is mapped to \(B'\) via \(p_{\theta}(x')\) (see Observation 2). This resorts to: